Microcontroller Math
For the 16 series microcontrollers I have been using in the past chapters there seems to be the only possibility to add or subtract. This page is to demonstrate that from just using adding and subtracting commands that you can infact multiply, divide, square and square root a number. Below are links to sections on this page.
Addition is one of the more simple commands on the microcontroller, below are three examples of adding numbers and variables. If the result overflows then the carry bit will flag in the status register, when flagged a third variable will be incremented. Since we are dealing with binary the highest number in 8-bit is 255, since the first bit in variable3 is equal to 256 it means that adding two variables of the value 255 will only result in a carry of one.

The above was an example of adding two 8-bit numbers, but what if we want to add an 8-bit to a 16-bit or 16-bit to 16-bit. Below is an example of how the program would do so in the first occasion. As you can see there is no difference to the above code as the lower 8-bits are added to the other lower 8-bits, if there is a carry then it will increment the higher 8-bit register resulting in a 16-bit result.

To add two 16-bit numbers quite simply the lower 8-bits are added first, if there is a carry then it will increment the higher register, if that register carries then it will increment the register above that. Next the second words are added, again if there is a carry then the word above that will be incremented.
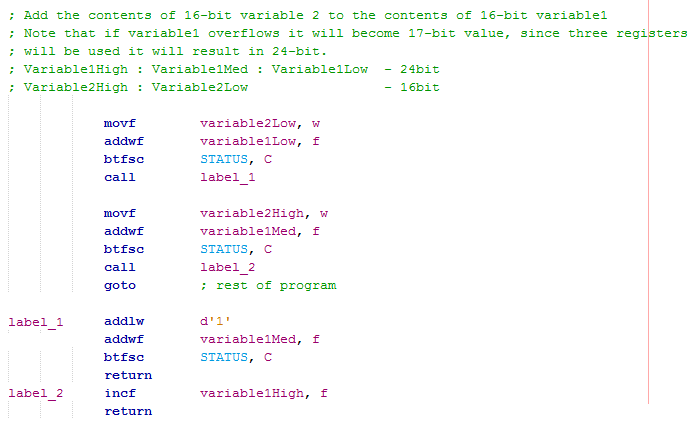
As you can see adding numbers is a very simple task, all that needs to be checked is if a carry has been created and whether it needs to increment the register above it. The only one rule is that bits 0 - 7 are added together, bits 8 - 15 are added together and so on, this should seem pretty obvious. One thing to take note is that the increment and decrement commands do not affect the carry flag, to increment a register and check the carry flag you must use an addition command.
Subtraction can seem a little awkward at first as you will soon see. To subtract a variable from another variable you must load the working register with the value you want to subtract. The awkward thing with subtracting is that if you want to subtract multiple variables from the working register then you must load the contents of the working register into a temporary variable, the variables to subtract must then be loaded one by one into the working register. Subtracting a constant value is the same process, there is however the option of subtracting a variable from a literal, the results are placed into working register. The confusion with the subtraction commands is that the carry bit is set after a subtraction is successful, the bit will clear if a borrow is required.
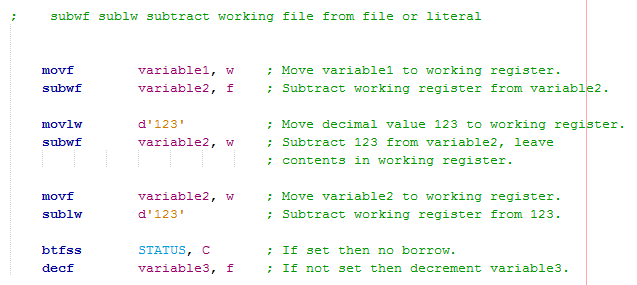
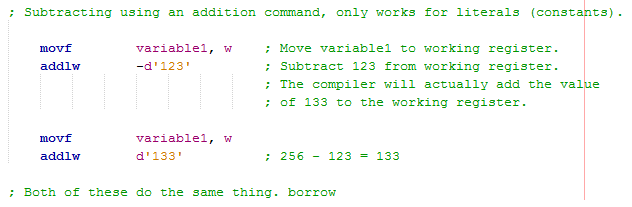
An alternative method is to use an addition command, this can only be used with literals as we known their value. Since the value of 8-bit is 256 quite simply by adding 256 minus the value to be subtracted you get the required value to add. Another option is to place a negative symbol in front of the literal, the compiler will work out the value to add. The carry bit will flag if the subtraction has been successful, if a borrow is required then the bit will not be set. This method can be more useful since the working register does not require a temporary variable, multiple literals can be subtracted from the working register with ease.
To subtract an 8-bit value from a 16-bit all that is required is a check to see when a borrow is required. When a borrow is required it will check to see if there is data there to borrow, if so it will decrement the register. If there is no data to borrow then we have a problem, this may result in an error for the application or may result in a negative symbol to be displayed on an LCD.

To subtract a 16-bit value from a 24-bit value the same procedure is utilised. The lower 8-bits are always processed before the higher level 8-bits to be able to check if a borrow is required.

You will notice that in the instruction set of a microcontroller that there are only commands for addition and subtraction and not any for multiplication. Multiplication can simply be done with addition, for example 4 x 3 is the addition of 4 three times or the addition of 3 four times. Below is an example of a program that does this. The main issue is that the multiplier determines how many times the program will cycle, variable1 in this case or temp, a clone of variable1 which acts as the counter. This may seem an easy method to use but becomes far too slow for numbers over 8-bit.

The method to use refers back to table multiplication and adds the numbers in a more efficient fashion, here is an example of how two binary numbers are multiplied together. When there is a zero in the digit no multiplication occurs, when there is a one then simply a value is shifted by how many digits from the right the number is at. All of the eight results are added together to get the product.

Here is a section of program that uses this exact method. If first checks whether the digit in the multiplier is a zero or a one, if a zero then it will skip the addition and go straight to rotating registers. If it is a one then the temporary registers are added to the output registers. Rotating the registers is just like adding zeros before the numbers, these are rotated left. The number to be rotated right is the multiplier as the program will check it's first bit to see if addition needs to take place, obviously if it is a zero then multiplying by zero results in zero, there is no point in the addition taking place.

An obvious solution would be to do as I did in the program above and follow the multiplication exactly. There is another method to use which does things backwards but is a lot more efficient at multiplication. If instead we add the number we are multiplying to the product high register and then rotate both registers right every multiplication then for each rotation we are removing a zero. So for example the first addition needs no zeros, it has eight to start with but is rotated right a total of eight times and therefore there is no zero present at the end. The next bit requires one zero, it starts off with eight and is rotated right a total of seven times and therefore ends with a zero. This section of program is really simple but effective in how it works.

Since the above program is quite long there is an alternative which cycles more times but has far less instructions and therefore saves memory space in the program. I prefer to use this method due to it's cleaner look, it does exactly the same job but instead of checking each individual bit in the multiplier we instead shift the multiplier and check the carry bit instead. By loading the most significant bit of the ProdL register (bit 7) first, after a total of eight cycles it will make it's way into the carry bit indicating that the multiplication has completed.
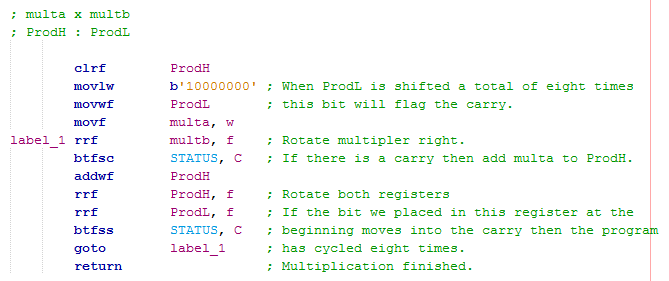
What if I want to multiply together two 16-bit numbers, well the process is quite similar. Instead of loading the variable to be multiplied into the working register, this time it must be accessed when we need it as we have to swap between the high 8-bits and the low 8-bits. The MSB is loaded in the second product register as a completion indicator, since we are dealing with 16 bits we must loop the program a total of 16 times.

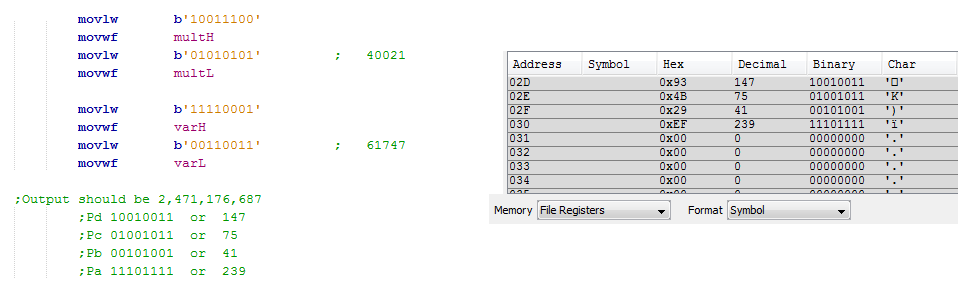
As a quick check I loaded the variables with the following values, ran a simulation and looked up the variables. As you can see they match so the process worked. I find this to be the easiest method to use with 16-bit multiplication, you can find many other examples out there to do the same thing but I believe this to be the most concise method.
Overall multiplication is all not that bad and can be done with relative ease and speed. It is quite cumbersome to use a program with more than four words so I believe that the above programs should be adequate for most projects. It is however quite easy to scale the program up to 32 bits if required.
Division is a very similar process to multiplication however this time you are subtracting multiple times. For example 9 divided by 3 is the same as 9 minus 3 three times, the difference is that you count the number of times you subtract until you reach zero or into minus. I'm going to give only one program example this time as there is no other better method for division.
This program is quite a commonly used method, it uses four words to make up the 32-bit number to be divided, the output number remains in these variables. The program works backwards to that of the multiplication, it rotates the registers left this time. When it rotates the registers it checks for a carry, if there is a carry it means a remainder was present and it needs to be dealt with. The remainder variables work like a working register to not disturb the data flow in the word variables. The denominator, the number we are dividing by is checked against the remainder variables to see if we will have a remainder, whether we need to borrow or otherwise continue with the program. The program will loop a total of 32 times until the process has been completed.

Division can be quite a difficult subject to deal with regards to microcontrollers, the above program proves it requires little code but has to loop twice the amount of times than that of multiplication, it is overall a slower process.
Quite simply you place the same values in the multiplication program, some have asked and here is the explanation.
It is a little more difficult to square root something and generally a lookup table is used in microcontroller applications. If you however require a mathematical approach then I will give a mathematical solution. I have covered division and addition which are both required for the method I will be choosing and that method is known as the "Babylonian Method". One thing to note with a square root is that it's not an exact equation and is made up of a series of approximations until the required degree of accuracy is met.
Here is the Babylonian method, all that is required is a number to square root and an approximation of that root. The approximation just has to be less than the number we need to root, the closer the approximation the less stages there are. As you can see by following the pattern the numbers start to match, it is up to the us how much accuracy is required. Since we are dealing with a microcontroller a division by two is enough of an approximation, the microcontroller works with whole numbers so in this case when it detects that two numbers are the same then the process has been complete, X4 and X5 are both 15, this would be detection. An alternative to a higher degree of accuracy is to multiply the starting number by 100, the square root would then need to be shifted one decimal place or a decimal point placed in an LCD if that is the method for displaying the data.

Here is the program which follows the Babylonian method, it should be quite easy to follow. You will notice that in this example I chose to loop the program a total of ten times since this is sufficient to find the root of the numbers that we are dealing with. The program will divide by two on a couple of occasions, to save on confusion I ran the division program but an easier way is to shift all of the registers right one place.

The number I chose to square root was 107414, using a caculator I get 327.74 to 2dp. Since the microcontroller only works in whole numbers and cannot differentiate between rounding up or down I would expect the result to be 327. As proof that the program works here is the output of the 32-bit register, 101000111 is equal to 327.
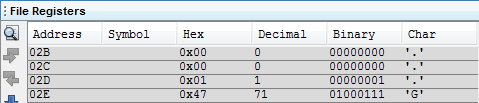
In all instances the root will be found in ten cycles, however there are many instances that the root will be found after just one cycle, for example 4. The program needs to compare the previous answer with regards to the current answer, if they match then the root has been found. For the example of 4 this would take two cycles. Below is the program.

I placed a counter in my program to see how many cycles it would need to veryify that a root has been found. As you can see for this example it took a total of eleven cycles, this meant that on the tenth cycle the root was found.

I hope that this page has cleared some understanding on microcontroller math or given you the template to do math in your own program. Please check out the other microcontroller tutorials and projects.
Hello, if you have enjoyed reading this project, have taken an interest in another or want me to progress one further then please consider donating or even sponsoring a small amount every month, for more information on why you may like to help me out then follow the sponsor link to the left. Otherwise you can donate any amount with the link below, thank you!